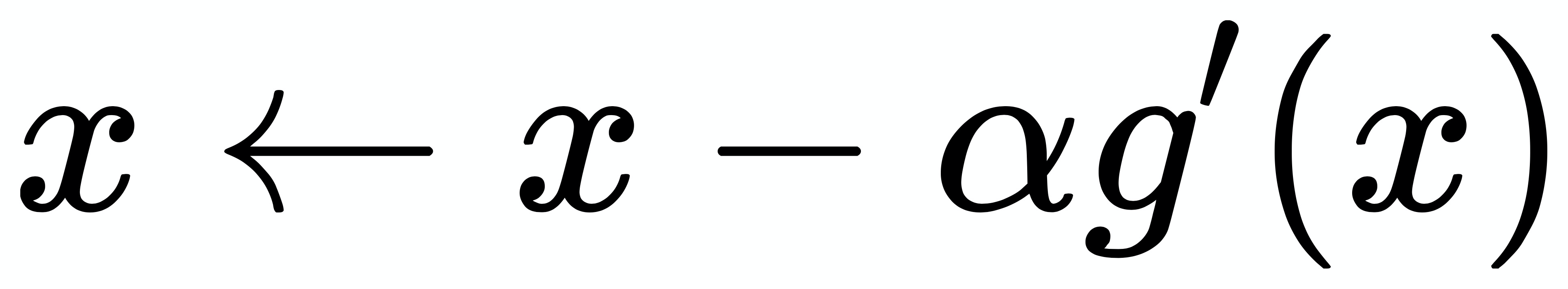2020 年春节将至，大部分同事已经回家。回顾下自己的 2019，似乎收获颇丰：不仅顺利毕业，还找了份谋生的工作。这期间看了很多复杂的算法，有监督 or 无监督，目标检测 or 深度估计。而人一旦徜徉在其中，就会渐渐忘记一些基础的东西。是时候回顾一下梯度下降法了….

问题：请尝试使用梯度下降法求解 sqrt{2020} 的值，并精确到小数点后 4 位。

思路：该问题等价于求函数 f(x) = x^{2} - 2020 的根，也就等价于求 g(x) = (x^{2} - 2020)^2 的最小值。所以，我们可以建立损失函数：

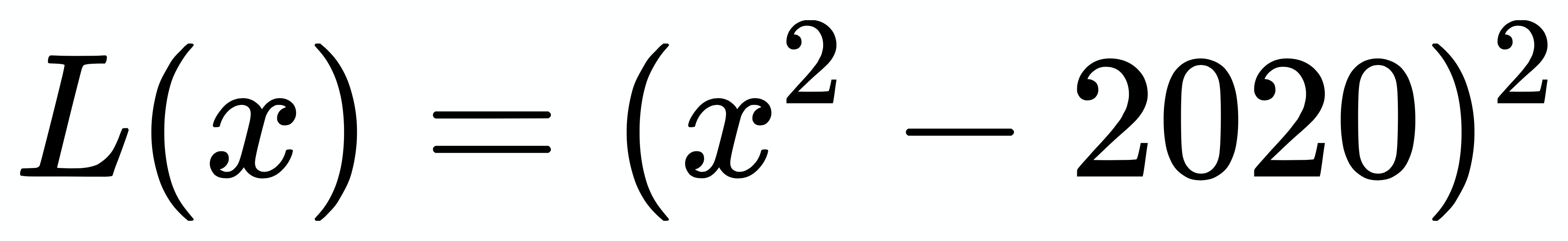
梯度下降法:

其中 a 为学习率，整个过程的代码如下：

import numpy as np

epochs = 100
lr = 1e-5
x  = 10

grad = lambda x: 4 * x * (np.power(x, 2) - 2020)
loss = lambda x: (np.power(x, 2) - 2020)**2

for epoch in range(epochs):
    x = x - lr * grad(x)
    print("=> epoch %2d, x=%.4f, loss = %.4f" %(epoch, x, loss(x)))

在整个过程中，我们只需要不断利用梯度下降法更新参数就可以了。最后训练损失曲线逐渐下降至 0， 此时得到的 $x$ 已经收敛至 44.9444，满足要求。

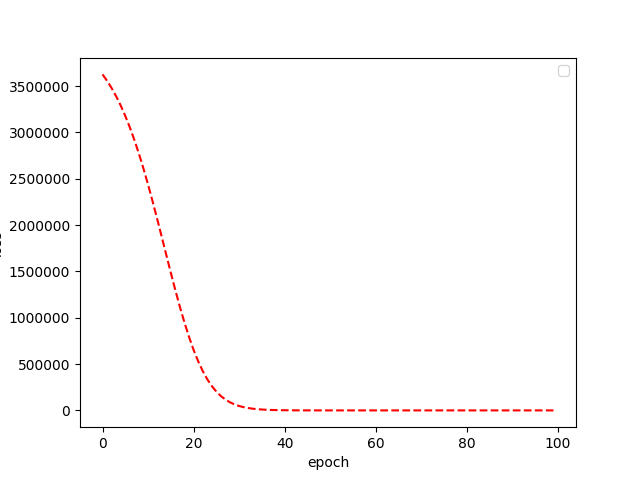
但事情并不总是一帆风顺，我也尝试了一些失败的案例：

  • 学习率过大的情况，当 x=10 而且 lr=1e-3 时

    => epoch  0, x=86.8000, loss = 30406842.7776
    => epoch  1, x=-1827.7441, loss = 11146440911634.0312
    ...
    => epoch 99, x=nan, loss = nan

  • x 的初始值过大的情况，当 x=2020 而且 lr=1e-5 时

    => epoch  0, x=-327513.1040, loss = 11505744027749453922304.0000
    => epoch  1, x=1405225186080.3201, loss = 3899273520282849001736422898828492926803876249600.0000
    ...
    => epoch 99, x=nan, loss = nan

希望能给大家调参带来一些启示。